Home » Archives for diciembre 2015
3 Comments

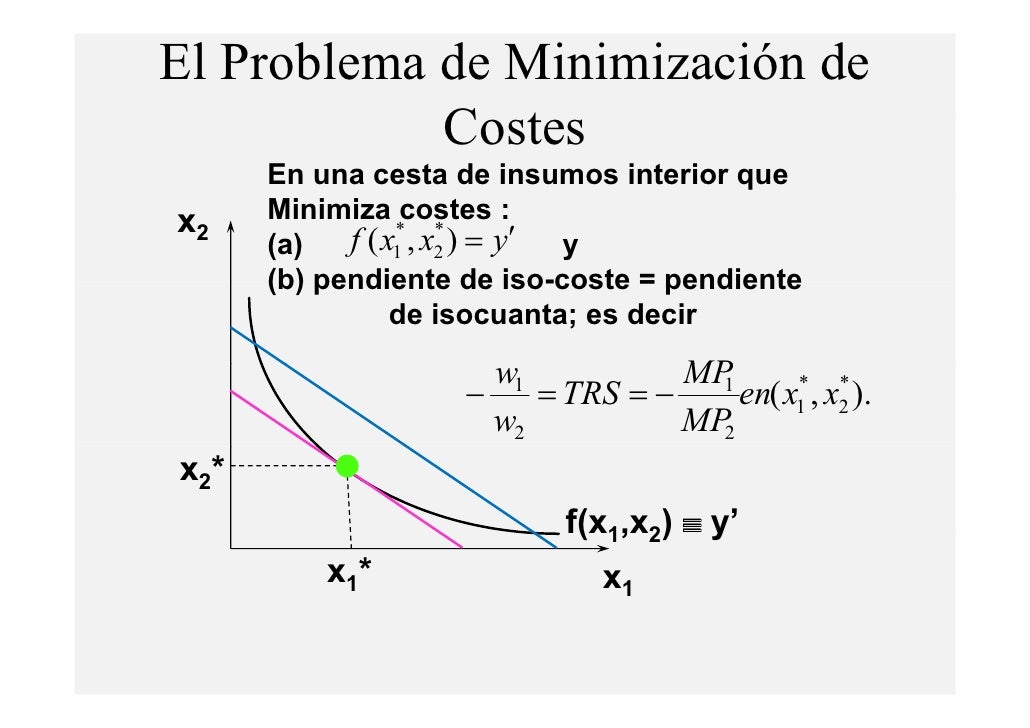
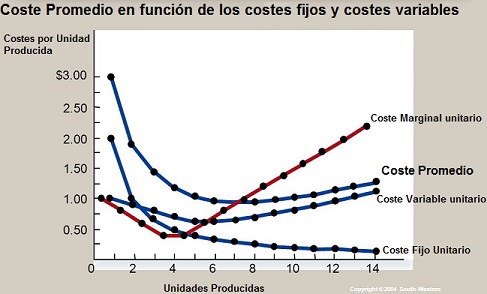
5.6 Elasticidades: elasticidad de la demanda y elasticidad del ingreso.

ELASTICIDAD PRECIO DE LA DEMANDA:
Es el grado de sensibilidad de la cantidad demandada ante una variación en el precio del bien.
COEFICIENTE DE ELASTICIDAD PRECIO DE LA DEMANDA:
Se puede calcular el coeficiente de elasticidad precio de la demanda, el cual muestra la variación relativa o porcentual que se daría en la cantidad demandada ante una variación de un 1% en el precio.
 
El coeficiente de elastidad siempre da negativo, pero para efectos de análisis se emplea su valor absoluto.
Aunque aquí solo se menciona la elasticidad precio, también es posible calcular la elasticidad ingreso y la elasticidad cruzada, lo cual consiste en un concepto similar, pero no con respecto a las variaciones en el precio del bien, sino con relación a las variaciones en el ingreso y en el precio de bienes relacionados, respectivamente. Para ver información sobre este tema vea elasticidad cruzada, elasticidad ingreso y elasticidad de la oferta.
TIPOS DE ELASTICIDAD PRECIO DE LA DEMANDA
  • ELÁSTICA: El coeficiente de elasticidad es mayor que uno.
  • UNITARIAMENTE ELÁSTICA: El coeficiente de elasticidad es igual a uno.
  • INELÁSTICA: El coeficiente de elasticidad es menor que uno.
Observe a continuación cómo se dan estos tipos de elasticidad precio de la demanda en diferentes curvas de demanda lineales.
ELASTICIDAD EN CURVAS DE DEMANDA LINEALES: son elásticas en precios arriba del punto medio e inelásticas debajo de él. Si se comparan dos curvas en la misma gráfica, la curva más plana es más elástica para cada nivel de precio.
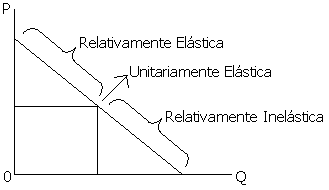
CURVAS DE DEMANDA VERTICALES: son perfectamente inelásticas. Ante una variación en el precio la cantidad sigue igual. El coeficiente de elasticidad precio de la demanda es cero. Este es el caso de bienes que no tienen sustitutos o bienes muy básicos. Por ejemplo: la sal, medicamentos, etc.
CURVAS DE DEMANDA RELATIVAMENTE INELASTICAS: Ante una variación en el precio la cantidad disminuye en una proporción menor. El coeficiente de elasticidad precio de la demanda es menor que uno. Este es el caso de bienes que tienen pocos sustitutos o algunos bienes básicos. Por ejemplo: la gasolina, etc.
CURVAS DE DEMANDA HORIZONTALES: son perfectamente elásticas. Ante una variación mínima en el precio la cantidad demandada será cero. El coeficiente de elasticidad precio de la demanda es infinito. Este es el caso de bienes que tienen sustitutos perfectos.
CURVAS DE DEMANDA RELATIVAMENTE ELASTICAS: Ante una variación en el precio la cantidad disminuye en una proporción mayor. El coeficiente de elasticidad precio de la demanda es mayor que uno. Este es el caso de bienes que tienen muchos sustitutos o algunos bienes suntuarios (bienes de lujo).

2 Comments

5.5 Optimización de funciones económico-administrativas: maximización de funciones de ingreso, utilidad y beneficios; minimización de funciones de costos y costos promedio.

Utilidad y beneficios.
El beneficio económico (también denominado utilidades) es un término utilizado para designar la ganancia que se obtiene de un proceso o actividad económica. Es más bien impreciso, dado que incluye el resultado positivo de esas actividades medido tanto en forma material o "real" como monetaria o nominal. (Ver más abajo). Consecuentemente, algunos diferencian entre beneficios y ganancia.
Desde un punto de vista general el beneficio económico es un indicador de la creación de riqueza o generación de mercaderías o valor en la economía de una nación. Eso no es siempre el caso para los individuos (ver más abajo).
El beneficio generalmente se calcula como los ingresos totales menos los costes totales de producción y distribución.

 
La minimización de costo.
 
 
 
Para minimizar los costos de producción de una determinada cantidad, una firma debe elegir el punto de la isocuanta en el que la relación de sustitución técnica de los factores sea igual al cociente del precio de los factores o costo de oportunidad.

COSTO PROMEDIO.

El costo promedio (también denominado coste unitario) es el costo de producción por unidad de producto, y se calcula dividiendo el total de los costos fijos y los costos variables por el número total de unidades producidas (producción total). La reducción de los costes medios son una potente ventaja competitiva.
Fórmula: (costos fijos + costos variables) / La producción total
 
 
 
coste promedio 
 
 
 




 
   






fuente:  http://daisy-gutierrez-mate1.blogspot.mx/p/5_49.html
No Comment

5.4 Concavidad, puntos de inflexión y prueba de la segunda derivada.

Criterio de la segunda derivada para establecer los valores máximos y
los valores mínimos de una función Además de proporcionar información sobre la concavidad de la gráfica de una función, la segunda derivada permite establecer si un punto crítico es un valor máximo o un valor mínimo. 
El siguiente teorema se refiere a este segundo aspecto.

 Teorema
 Sea f una función con dominio D.

Si $f'(x)$ está definida para $x \in ]a,b[$ donde $]a,b[ \subset D$ y si $f'(x_{0})=0$ con$x_{0} \in ]a,b[$ entonces:
a.
 		$f(x_{0})$ es un valor máximo relativo de f si se cumple que $f''(x_{0})<0$
b.$f(x_{0})$ es un valor mínimo relativo de f si se cumple que $f''(x_{0})>0$
  Demostración: Al final del capítulo.
 
Ejemplos: 

Utilizando el teorema anterior vamos a determinar los valores máximos y los valores mínimos de las funciones cuyas ecuaciones son:

1.   $f(x)=\displaystyle\frac{x^2}{x+1}$, $x \in ]-4,2[$
Note que la función f no está definida en $x=-1$ 

La derivada de f está dada por $f'(x)=\displaystyle\frac{x(x+2)}{(x+1)^2}$, $x \neq -1$ 

Los valores críticos de f se obtienen cuando $f'(x)=0$. En este caso, $f'(x)=0$ si y solo si $x=0$, ó $x=-2$. 

Ahora, la segunda derivada de f es $f''(x)=\displaystyle\frac{2}{(x+1)^3}$ 

Vamos a evaluar $f''(x)$ en $x=0$ y en $x=-2$  
a.$f''(0)=2$; como $2 > 0$ entonces $f(0)$ es un valor mínimo relativo de f.  
b.
 		$f''(-2)=-2$; como $-2<0$ entonces $f(-2)$ es un valor máximo relativo def.
Gráficamente se tiene en el intervalo $]-4,2[$ 
2.
Se tiene que $D_{g} = I \! \! R$ 

La primera derivada de g está dada por  


Como $g'(x)=0$ cuando $x=1$ y cuando $x=6$ entonces estos son los valores críticos de g. 

La segunda derivada de g es $g''(x)=\displaystyle\frac{5(x-3)}{3\sqrt[3]{x-1}}$ 

Evaluando $g''(x)$ en $x=6$ se tiene que   
 que es mayor que cero, por lo que $g(6)$ es un valor mínimo relativo de g. 

Observe que $g''$ no puede evaluarse en $x=1$ pues hace cero el denominador por lo que para este valor crítico debe utilizarse el criterio de la primera derivada. 

Analizando $g'(x)=(x-1)^\frac{2}{3} (x-6)$ se obtiene que $g'(x)<0$ para $x \in ]-\infty,1[$ y $g'(x)<0$ para $x \in ]1,6[$por lo que al no existir cambio de signo resulta que $f(1)$ no es ni máximo ni mínimo. El gráfico de g se muestra a continuación. 


Fuente; http://daisy-gutierrez-mate1.blogspot.mx/p/5_98.html