Calculo del Interés Compuesto
Para un período de tiempo determinado, el capital final (CF) se calcula mediante la fórmula
Ahora, capitalizando el valor obtenido en un segundo período
Repitiendo esto para un tercer período
y generalizando a n los períodos, se obtiene la fórmula de interés compuesto:
Donde:
 es el capital al final del enésimo período
es el capital al final del enésimo período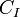 es el capital inicial
es el capital inicial es la tasa de interés expresada en tanto por uno (v.g., 4 % = 0,04)
es la tasa de interés expresada en tanto por uno (v.g., 4 % = 0,04) es el número de períodos
es el número de períodos- Límite de la función costo promedio.
- En la Economía también es importante considerar la variación de una cantidad respecto a otra. Por ejemplo la demanda de un producto respecto a su precio, o el precio de un producto respecto a su costo de producción o la utilidad obtenida en la venta de un producto, con relación al costo de producción, etc.Por lo anterior, es muy importante la representación de las cantidades relacionadas en forma de funciones que puedan ser derivables, no obstante que los datos que se manejan sean discretos, por ejemplo cuando se establece la función de costo
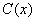 , la variable x representa unidades de cierta mercancía.En Economía se suele describir la variación de una cantidad respecto a otra mediante un concepto llamado promedio que expresa la variación de una cantidad sobre un rango específico de valores de otra y un concepto llamado marginal que expresa el cambio instantáneo en una cantidad respecto a la otra.Un símil de los conceptos anteriores en Física serían los conceptos de velocidad promedio y velocidad instantánea o lo que geométricamente serían la pendiente de la recta secante y la pendiente de la recta tangente, respectivamente.
, la variable x representa unidades de cierta mercancía.En Economía se suele describir la variación de una cantidad respecto a otra mediante un concepto llamado promedio que expresa la variación de una cantidad sobre un rango específico de valores de otra y un concepto llamado marginal que expresa el cambio instantáneo en una cantidad respecto a la otra.Un símil de los conceptos anteriores en Física serían los conceptos de velocidad promedio y velocidad instantánea o lo que geométricamente serían la pendiente de la recta secante y la pendiente de la recta tangente, respectivamente.- Un ejemplo:
- Si
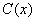 es la función que representa el Costo Total en unidades monetarias para producir x unidades de cierta mercancía:
es la función que representa el Costo Total en unidades monetarias para producir x unidades de cierta mercancía: - El costo promedio de producción de cada unidad, sería el costo total entre la cantidad de unidades de mercancía producidas, es decir:
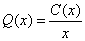 , a la cual se le llama función del Costo Promedio.
, a la cual se le llama función del Costo Promedio. - El costo marginal cuando
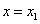 es
es 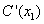 , si esta cantidad existe. Y se interpreta como la razón de cambio instantánea del Costo Total con respecto al cambio unitario en las unidades producidas, cuando se producen
, si esta cantidad existe. Y se interpreta como la razón de cambio instantánea del Costo Total con respecto al cambio unitario en las unidades producidas, cuando se producen 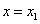 unidades.
unidades. - De manera similar
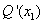 sería el Costo Promedio Marginal cuando
sería el Costo Promedio Marginal cuando 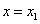 y que representa la razón de cambio instantánea del Costo Promedio cuando
y que representa la razón de cambio instantánea del Costo Promedio cuando 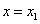
- Fuente:http://matematicasrobles.blogspot.mx/2015/05/26-aplicaciones-las-ciencias-economico.html
- Si

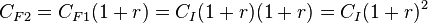

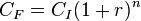
0 Comments